Ya tenemos la idea, ahora tenemos que implementarla. El presupuesto rondará los 110€ a los que habrá que sumarle los gastos de envío a certificado a Noruega. El plazo aproximado de ejecución será de unos 15 días invirtiendo alrededor de 50 horas de trabajo.
Esperamos tenerlo finalizado y listo para enviarlo el 11 de Septiembre.
Empezaremos por conseguir la pieza más importante, el GPS.Sus prestaciones no son para nada destacables, sus tiempos de arranque y readquisición son bastante pobres, pero es barato, fácil de conseguir, cuenta con conexión serie tanto RS-232 como LVTTL (0-3.3v), consume tan sólo 110mW alimentado entre 3.8v y 8.0v, y sólo pesa 14 gramos (34.0mm x 34.0mm x 8.6mm).
El microcontrolador, el autentico motor del Latinómetro, es a su vez el elemento más barato y fácil de conseguir. Utilizaremos uno de los nuevos microcontroladores con CPU de 8 bits hasta 48Mhz y controlador USB incorporado de la casa Microchip, concretamente el modelo de 28 pines 18LF2550, variante de bajo voltaje capaz de funcionar con tan sólo 2.0 voltios.
Para que el acabado final sea lo más profesional posible, reutilizaremos un estuche originalmente pensado para contener una consola Nintendo DS de gran calidad de la marca MadCatz. El espació hábil para ubicar nuestros componentes será el mismo de la NDS; 148.6mm de ancho, por 84.6mm de alto, por 28.7mm de grosor.
La única parte software del Latinómetro será el firmware que ejecutará el microcontrolador. Su desarrollo se realizará en C, utilizando el compilador integrado en el IDE de desarrollo de CCS.
Ha aparecido una voz discordante que propone que se lo enviemos para el día de su cumpleaños, al parecer el próximo 9 de Noviembre. Ya veremos los comentarios al respecto.
O simplemente NMEA es el protocolo de conexión de instrumentos de navegación marítima definido por la asociación estadounidense sin animó de lucro National Marine Electronics Association. Su primera versión se publicó en Marzo de 1983 y su última revisión (v3) a finales del 2001.Para nuestro propósito sólo necesitamos obtener del dispositivo GPS (ID=GP), los valores de la sentencia MRC (Recommended minimum specific GPS/Transit data), cuyo formato para la v3 de NMEA es el siguiente:
$GPRMC,hhmmss.ss,A,llll.ll,a,yyyyy.yy,a,x.x,x.x,ddmmyy,x.x,a,m*hh
Field #
01 = UTC time of fix
02 = Data status (A=Valid position, V=navigation receiver warning)
03 = Latitude of fix
04 = N or S of longitude
05 = Longitude of fix
06 = E or W of longitude
07 = Speed over ground in knots
08 = Track made good in degrees True
09 = UTC date of fix
10 = Magnetic variation degrees (Easterly var. subtracts from true course)
11 = E or W of magnetic variation
12 = Mode indicator, (A=Aut., D=Diff., E=Estim., N=Invalid)
13 = Checksum
Las coordenadas geográficas eclípticas, Latitud y Longitud, vienen expresadas en grados y minutos con decimales sexagesimales, junto al hemisferio o lado del ecuador de dirección, por lo que habrá que convertirlas a coordenadas absolutas.
Es decir, en una sentencia como esta:
$GPRMC,154653,V,4428.2011,N,00440.5161,W,000.5,342.8,050407,,,N*7F
Tenemos una latitud de 44 grados con 28.2011 minutos al Norte, y una longitud de 4 grados con 40.5161 minutos al Oeste, que convertidas a valores absolutos serían:
Un punto en mitad del mar Cantábrico......
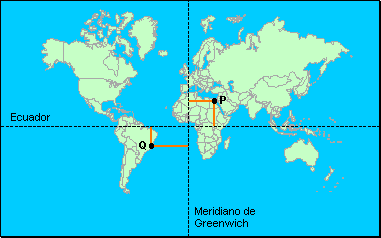
Estas dos coordenadas geográficas indican la distancia en grados sexagesimales desde el punto en cuestión hasta las líneas base de referencia; el paralelo cero o Ecuador para la Latitud, y el meridiano cero o meridiano de Greenwich para la Longitud.
Para la Latitud, sabiendo que la circunferencia que corresponde al Ecuador mide 40076 km, 1º equivale a 113.3 km.
Para la Longitud, sabiendo que junto con sus correspondientes antimeridianos se forman circunferencias de 40007 km de longitud, 1º equivale a 111.11 km.
A veces es conveniente usar en diversos problemas el concepto de Colatitud, que es el complemento de la latitud a 90º, es decir es el ángulo que forma la vertical del lugar con el eje Norte-Sur, o bien, dicho de otro modo, el arco de meridiano terrestre comprendido entre el lugar y el polo geográfico más próximo. Es evidente, en definitiva, que para un lugar cualquiera de la superficie terrestre es: Latitud + Colatitud = 90º.
La distancia entre dos puntos, P y P' de la superficie de la Tierra es la longitud del arco de círculo máximo comprendido entre el punto P y el punto P'. Para hacer estos cálculos aproximaremos el elipsoide terrestre por la forma esférica, y calcularemos el arco de círculo máximo entre ambos puntos mediante la fórmula de los cosenos de la trigonometría esférica.
Sean los puntos P y P' dados por sus coordenadas:
| dPP' = | 40000 | αPP' |
| 360 |
| dPP' = | 40000 | arc cos [cos φ · cos φ' + sen φ · sen φ' · cos (λ - λ')] |
| 360 |
El Rumbo a seguir para desplazarse por un arco de círculo máximo desde el punto P al punto P' cumple el teorema de los senos:
| sen NPP' | = | sen (λ - λ') | -> NPP' = | sen φ' · cos (λ - λ') | |
| sen φ' | sen dPP' | sen dPP' |
Se tiene en definitiva:
| rumbo = NPP' = arc sen | sen φ · sen (λ - λ') | ||
| sen dPP' |
| rumbo = arc sen | sen φ · sen (λ - λ') | ||
| sen [ arc cos [cos φ · cos φ' + sen φ · sen φ' · cos (λ - λ')]] |
De esta forma tan sencilla podemos calcular la distancia y el rumbo entre dos puntos cuyas coordenadas geográficas son conocidas.
Menudo chasco, y yo que pensaba que las paradas de La Latina y Opera estaban juntas.
Hola a todos,
gracias de nuevo por este magnifico recuerdo que nunca podre olvidar, os lo garantizo :)
Perdonadme por la tardanza, pero he estado super liado y he tenido un problema con las pilas ya que ha estado encendido todo el viaje de vuelta, pero al fin lo he probado.
La distancia que nos separa es de 2.388,5 KM. Las fotos que os adjunto son desde el lugar donde trabajo. He dejado el latinometro en mi mesa, al lado del ordenador. Lamentablemente no funciona dentro de edificio. Pero cuando este agobiado, especialmente por la gente tan sosa y rara con la que trabajo ahora (claro que después de estar con vosotros estoy seguro que no voy a encontrar gente igual en ningún otro lugar), puedo salir a la terraza y encender mi latinometro, fumarme un cigarrito de los mios y pensar que estáis a unos 2.388 Km en la dirección que me indique mi querido LATINOMETRO.
Gracias a todos, no solo por este regalo, sino por el regalo que ha sido conoceros, trabajar y hacer cosas juntos. Cada vez que pase por Madrid estad seguros que os avisaré para intentar veros.
Un abrazo a tod@s, TOD@S.
PD: No veáis como hipnotiza mirar la circunferencia de leds mientras busca señal...
Ángel
